Describe How You Use Algebra to Determine Inverse Functions
Determine the domain and range of an inverse function and restrict the domain of a function to make it one-to-one. The notation f 1 f 1 is read f f inverse.

Openalgebra Com Inverse Functions
That means fleft x right and gleft x right are not inverses.
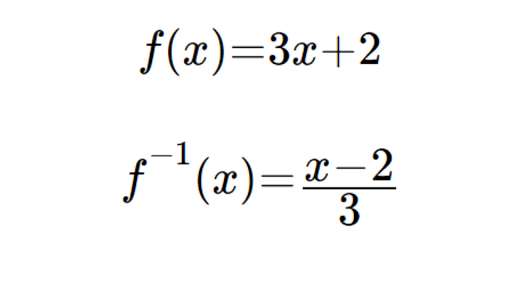
. A function that consists of its inverse fetches the original value. An inverse function goes the other way. The inverse of a function is denoted by f-1x and its visually represented as the original function reflected over the line yx.
Determine the domain and range of the inverse of a function. F x 3 x 2. Thus the function is one-to-one and has an inverse function.
If true move to Step 2. The square root function is the inverse of the square function. This video explains inverse functions.
How to Determine Whether Two Functions Are Inverses. Its ok the leave the left side as x47. If youre seeing this message it means were having trouble loading external resources on our website.
Plug gleft x right into fleft x right then simplify. Once youve found one composition that doesnt work youre done. If a function is not one-to-one you will need to apply domain restrictions so that the part of the function you are using is one-to-one.
Find or evaluate the inverse of a function. It is much easier to find. To find the inverse of a function you can use the following steps.
Next lets substitute our answer 18 into our inverse function for x. The inverse function returns the original value for which a function gave the output. 52 Inverse Functions.
Lets substitute 4 for x in our original equation. We are tempted to use the notation f-1 for the inverse function to f and we often do this. We find the domain of the inverse function by observing the vertical extent of the graph of the original function because this corresponds to the horizontal extent of the inverse function.
First is the question of notation. The inverse of f x7x-4 is f-1 x x47. A foundational part of learning algebra is learning how to find the inverse of a function or fx.
I didnt end up with just x so f x and g x are not inverses of each other. At the end of this section students will be able to. The inverse is usually shown by putting a little -1 after the function name like this.
For example find the inverse of fx3x2. Once you have y by itself you have found the inverse of the function. Y 3 x 2.
We find the domain of the inverse function by observing the vertical extent of the graph of the original function because this corresponds to the horizontal extent of the inverse function. It explains how to find the inverse function by switching the x and y vari. Like any other function we can use any variable name as the input for f 1 f 1 so we will often write f 1x f 1 x which we read as f f inverse of x.
We denote gx g x the inverse of fx f x by gxf1x. Find the inverse of a function. This concept has three complications that you must learn to handle.
Learn how to find the formula of the inverse function of a given function. What they are the notation used and the mathematical definition. Similarly we find the range of the inverse function by observing the horizontal extent of the graph of the original function as this is the vertical extent of the inverse function.
We find the domain of the inverse function by observing the vertical extent of the graph of the original function because this corresponds to the horizontal extent of the inverse function. G x f 1 x. If fgx x f g x x and gfx x g f x x then we say that fx f x and gx g x are inverses of each other.
Inverse functions in the most general sense are functions that reverse each other. Similarly we find the range of the inverse function by observing the horizontal extent of the graph of the original function as this is the vertical extent of the inverse function. Solve the equation from Step 2 for y y.
Let us start with an example. This algebra video tutorial provides a basic introduction into inverse functions. Let fx f x and gx g x be two one-to-one functions.
X y 2 3 1 x y 2 3 1 Show Step 3. So the inverse of. Replace every x in the original equation with a y and every y in the original equation with an.
No horizontal line intersects the graph in more than one place. Determine if a function has an inverse. For the first step we simply replace the function with a y y.
If you consider functions f and g are inverse f g x g f x x. Take the function equation and replace fx by y. There is also an example of how to show that 2 func.
Function takes to to and to. A typical example of inversion is the square root. In the original equation replace fx with y.
Y x 2 3 1 y x 2 3 1 Show Step 2. F x 2x. The final step is to rearrange the function to isolate y get it by itself using algebra as follows.
For example here we see that function takes to to and to. Use the graph of a one-to-one function to graph its inverse function on the same axes. The inverse of denoted and read as inverse will reverse this mapping.
Keep in mind that. If you found the correct inverse you should be able to plug the result into the inverse function and get your original x-value as the result. A reversible heat pump is a climate-control system that is an air conditioner and a heater in a single device.
This gives us fx 54 - 2 or fx 18. Determine algebraically whether f x 3 x 2 and g x 1 3 x 2 are inverses of each other. If we do this we get y 18 25 which simplifies to y 205.
F-1 y We say f. Verifying if two functions are inverses of each other is a simple two-step process. Similarly we find the range of the inverse function by observing the horizontal extent of the graph of the original function as this is the vertical extent of the inverse function.
Input the first function you are testing into your original function. The Inverse Function goes the other way. Next replace all the x x s with y y s and all the original y y s with x x s.
Ill plug the formula for g x into every instance of x in the formula for f x. F1x 1 fx f 1. Use order of operations to.
Graph the function and apply the Horizontal Line Test to determine if the function is one-to-one and thus has an inverse function. Inverse of a Function. Here we have the function fx 2x3 written as a flow diagram.

Inverse And Composite Functions Boundless Algebra

Introduction To Inverse Functions Youtube

How To Find An Inverse Function Inverse Functions Algebra Life Hacks

Finding Inverse Functions Quadratic Example 2 Video Khan Academy

How To Algebraically Find The Inverse Of A Function 5 Steps

19 Find The Inverse Of The Function F X X 8 5 Youtube

Openalgebra Com Inverse Functions

Inverse Of Linear Function Chilimath
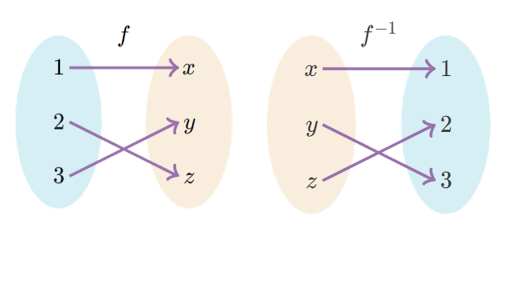
Intro To Inverse Functions Article Khan Academy
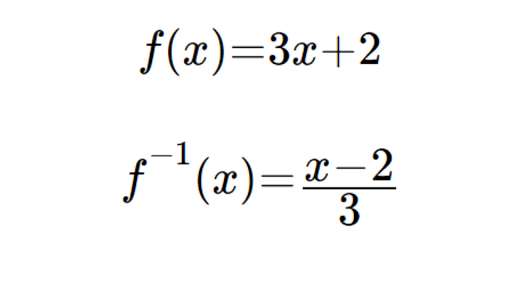
Finding Inverse Functions Article Khan Academy
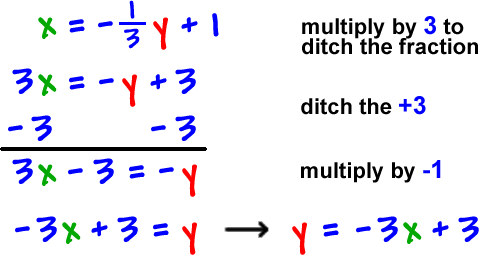
How To Find The Inverse Of A Function 1

How To Find The Inverse Of A Function Youtube
How To Find And Graph The Inverse Of A Function Algebra 2 Math Video Youtube

Verifying Inverse Functions Youtube

Derivative Of Inverse Functions How To W Examples


